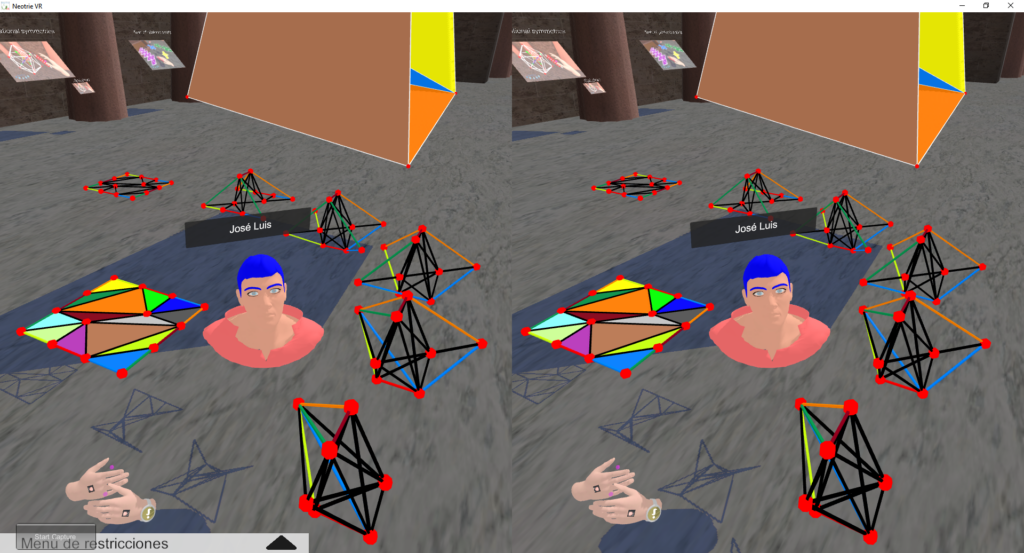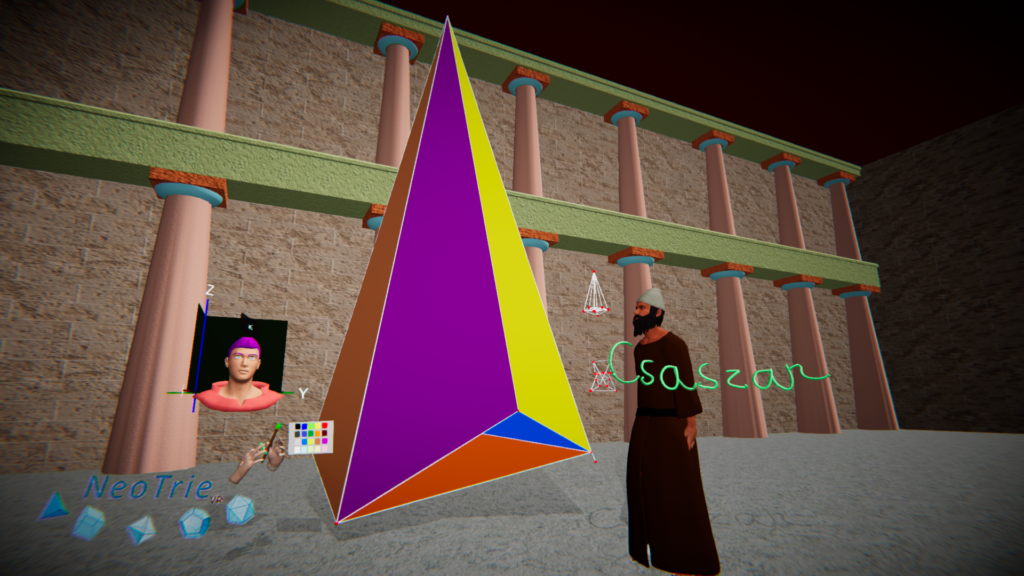
The Császár polyhedron is the first polyhedral realization of a torus with 7 vertices, without diagonals and without self-intersections (Császár, 1949), with 21 edges and 14 triangular faces.
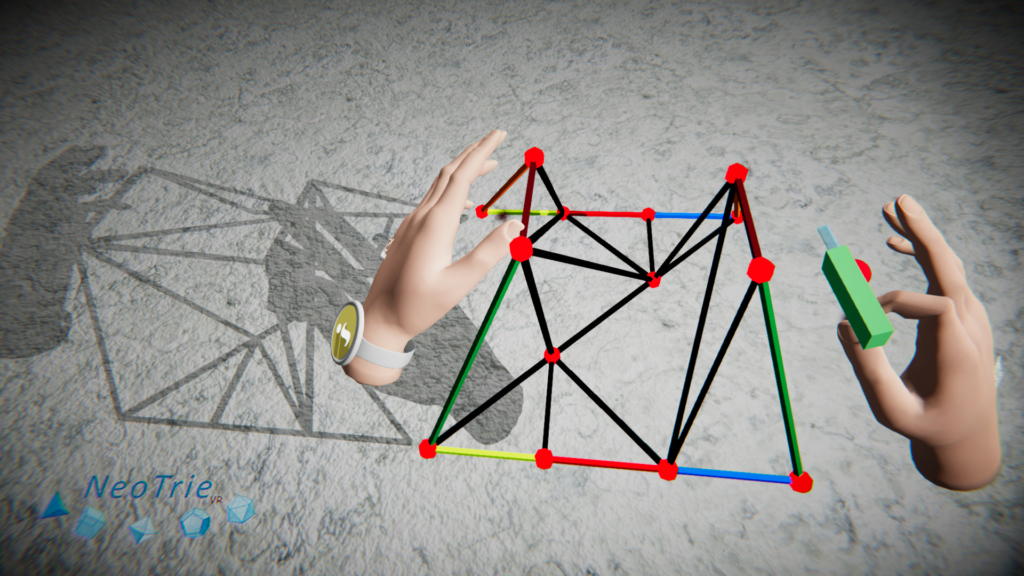
The 1-skeleton is the complete graph on 7 vertices. So we can manipulate it to get the graph of the Csaszar’s polyhedron. One can construct this model of the torus as the quotient of a square, and build step by step the construction. There is a last option to say Csaszar in high voice (or Csaszar with faces (on PC version)) to get the polyhedron automatically on the scene, thanks to the Speech Recognition System of Neotrie. One can enlarge the figure, and visit it from the inside, fly through the hole of the torus and see its interior too.




Demonstrations of Neotrie in Paris
Last week we visited the “Palais de la Découverte” and the “Cité des Sciences” in Paris, invited by Guillaume Reuiller.
During two days we were testing Neotrie VR and planning future collaborations with members and responsibles of Universcience, Science Ouverte, teachers of GIPTIP, and “Comité de Culture Mathématique de l’Institut Henry Poincaré”. It was a motivating and great experience! I would like to thank them here for their interest on Neotrie VR and its future applications and uses.
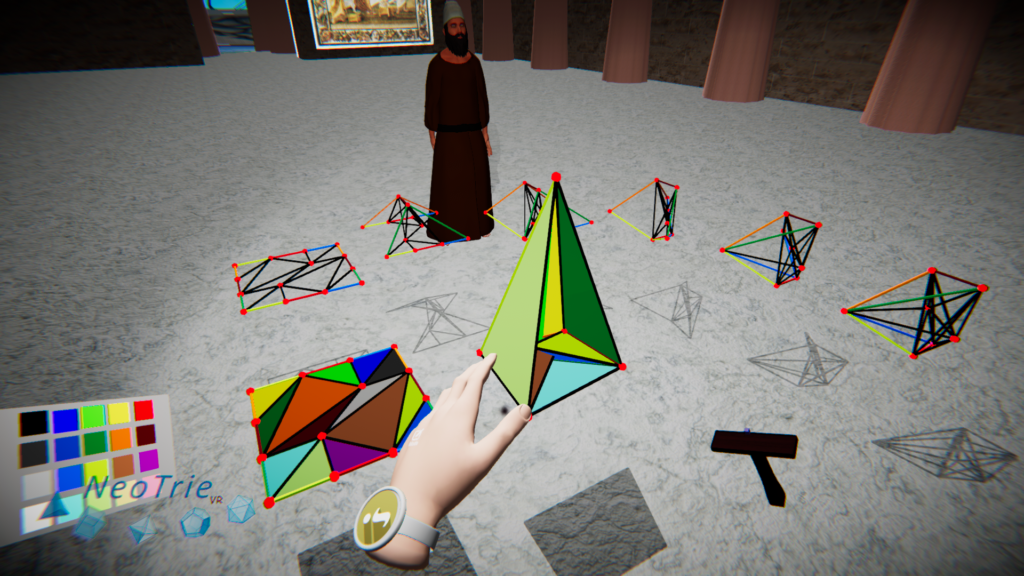
The activity of the Császár’s polyhedron was one of the VR experiences started by Roger Mansuy (second of the right in the next picture). We have completed this in this post.

ptr 
ptr 
cof 

edf
Downloads:
- csaszar.neot
Download this file to your local pc folder c:/documents/Neotrie/NeotrieSaves, and open it from the windows file system inside the temple. Try to move and glue the edges of the torus to build the Császár’s polyhedron. - csazar4.neot this is the final result, where you can enlarge the polyhedron and fly through the narrow hollow of the figure.
References:
- J. Bokowski and A. Eggert:Toutes les réalisations du tore de Moebius avec sept sommets, Topologie Struct. 17 (1991), 59-78.
- A. Császár: A polyhedron without diagonals, Acta Sci. Math., Szeged 13 (1949-1950), 140-142.
- F.H. Lutz, Császár’s Torus, Electronic Geometry Models: 2001.02.069.
- https://en.wikipedia.org/wiki/Cs%C3%A1sz%C3%A1r_polyhedron
- https://www.gaussianos.com/el-sorprendente-poliedro-de-csaszar/
Updated (4 January, 2019):
Here is the review by Roger Mansuy on the next nr 111 of Quadrature.