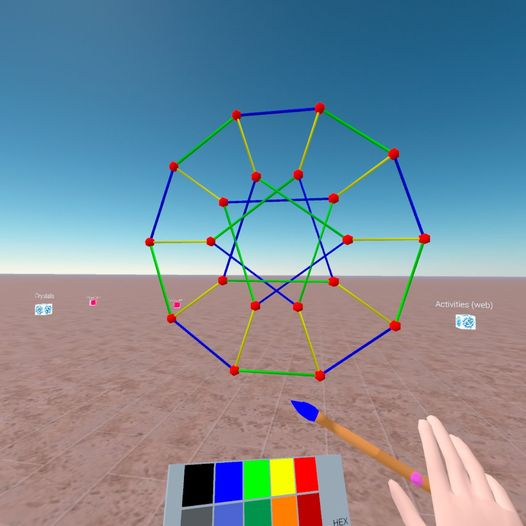
La 8ª Edición del Festival Internacional de Les Maths en Scène se ha celebrado del 14 al 16 de marzo de 2024. Un año más, hemos tenido la oportunidad de participar en esta fantástica fiesta matemática, impartiendo talleres de geometría en realidad virtual. En esta ocación, adaptamos a un taller la actividad sobre grafos que propusimos en la pasada noche de los investigadores https://www2.ual.es/neotrie/noche-europea-de-los-investigadores-2023/. Así, en grupos de unos 16 alumnos, de entre 13 y 16 años, practicaron primero con fichas plastificadas y rotuladores borrables, para seguidamente pasar a jugar en Neotrie con los 3 problemas más conocidos sobre grafos: encontrar el camino euleriano más largo, encontrar el camino o ciclo hamiltoniano más corto, y colorear un grafo con el mínimo número de colores.


Para facilitar el juego en Neotrie, preparamos una escena con una selección de grafos, la cual es accesible ya desde la caja de Activities (web). Los grafos de la escena están duplicados para permitir que haya dos jugadores realizando la actividad simultáneamente, a modo de competición, o colaborativamente. También es útil para un solo jugador que haya dos copias, para repetir un recorrido, si este no es el mejor encontrado.
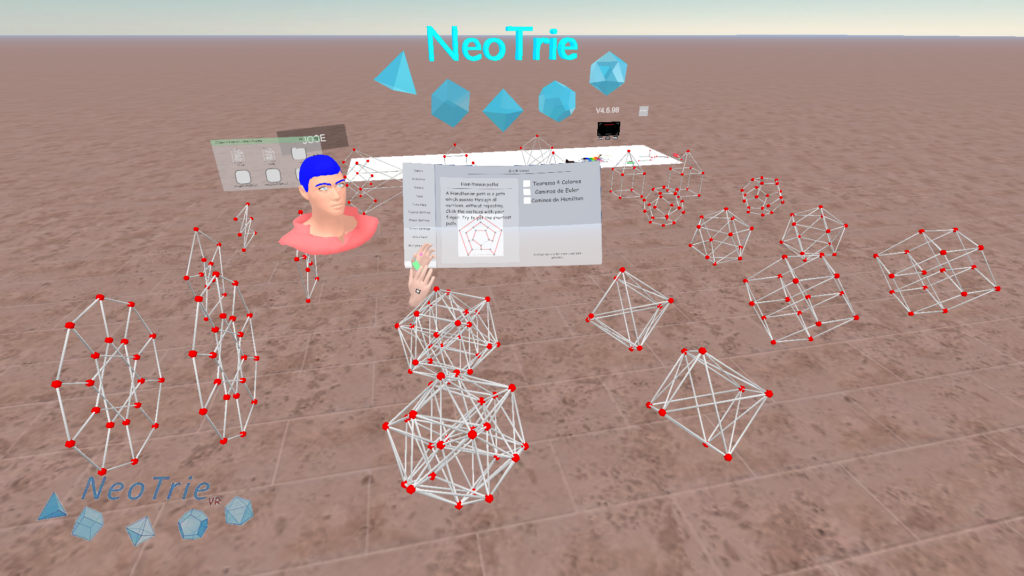
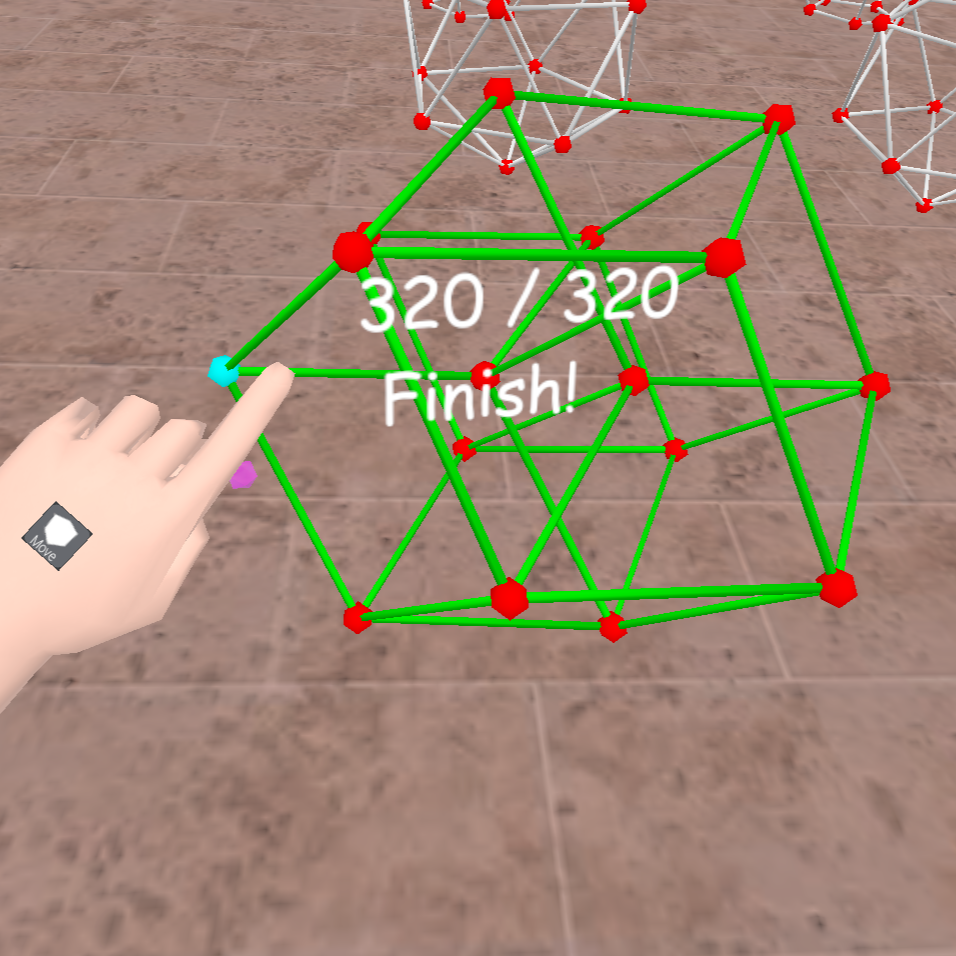
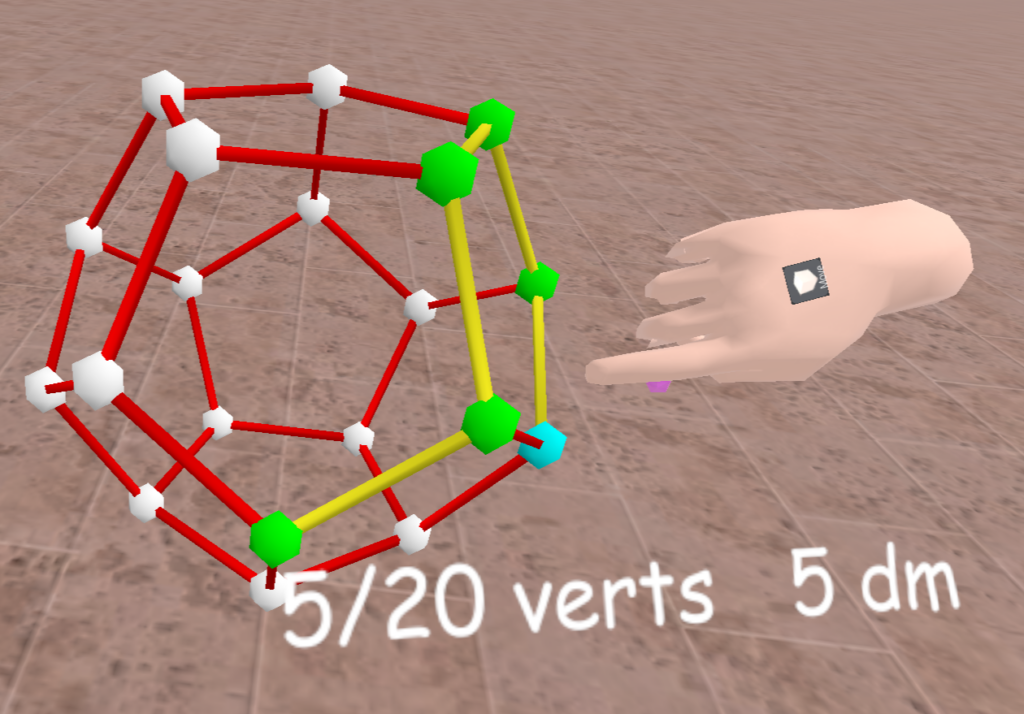

Continuaremos mejorando esta actividad, incorporando nuevas actividades, como por ejemplo la de colorear las aristas de un grafo: