En este video, dedicado a mí admirada Clara Grima, se proponen 3 actividades bien conocidas de grafos, para realizar no en el plano, como es habitual, sino en el espacio dentro de Neotrie VR.

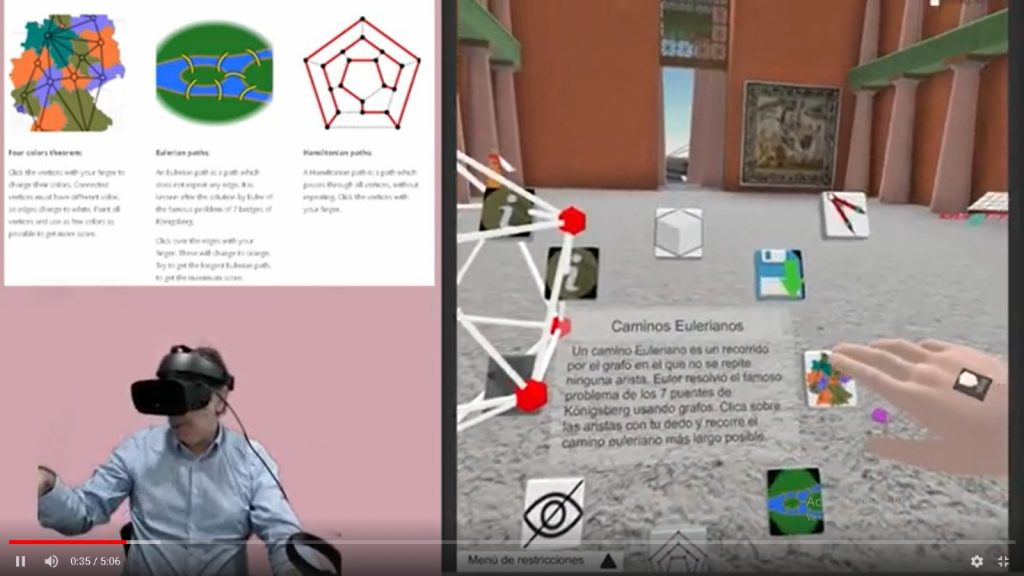
Dual del teorema de los 4 colores: En el espacio, los grafos pueden necesitar más de 4 colores, pero en el caso del icosaedro bastan 4, porque este es planar (puede aplanarse mediante su diagrama de Schlegel). Se puntúa más cuantos más vértices se coloreen (el rojo inicial no debe contarse, hay que colorear todos) y cuantos menos colores se utilicen. Cuando dos vértices tienen colores diferentes la arista que los une cambia de roja a blanca. La fórmula aplicada para calcular dicha puntuación (podría aplicarse otra) es:

Puntuacion = vértices coloreados + 10* (aristas blancas) / (aristas rojas + 10)

Una vez que todas las aristas son blancas, puntuacion = puntuacion * 5;

Caminos eulerianos: En esta actividad se van tocando las aristas para lograr el camino más largo sin salirse del grafo, que no pase dos veces por la misma arista. Recordemos, que un grafo es Euleriano si hay exactamente dos vértices de grado impar (es decir, concurren un número impar de aristas), o todos los vértices tienen grado par.

Caminos hamiltonianos: Es el conocido problema del viajante. Aqui hay que intentar pasar por el mayor número posible de vértices sin repetir ninguno, para lograr la máxima puntuación.

Otro problema implementado en Neotrie, que no se explica en este vídeo, es encontrar el camino más corto entre dos puntos, que soluciona el algoritmo de Dijstra. Este se logra usando la herramienta selección y manteniendo pulsado el gatillo al tocar dos vértices de una figura.

Recomendamos seguir a @ClaraGrima en redes sociales para saber más sobre grafos. No te pierdas su último libro “En busca del grafo perdido”.