En esta actividad, disponible en la caja de Erasmus Geometrician’s Views, realizamos una espiral pitagórica en el espacio con las herramientas de perpendicularidad y compás. La construcción es dinámica y podemos modificar algunos parámetros. A diferencia de la construcción en el plano, esta es más compleja, por no haber una única perpendicular a una recta en el espacio.

A continuación podemos ver cómo se ha hecho:

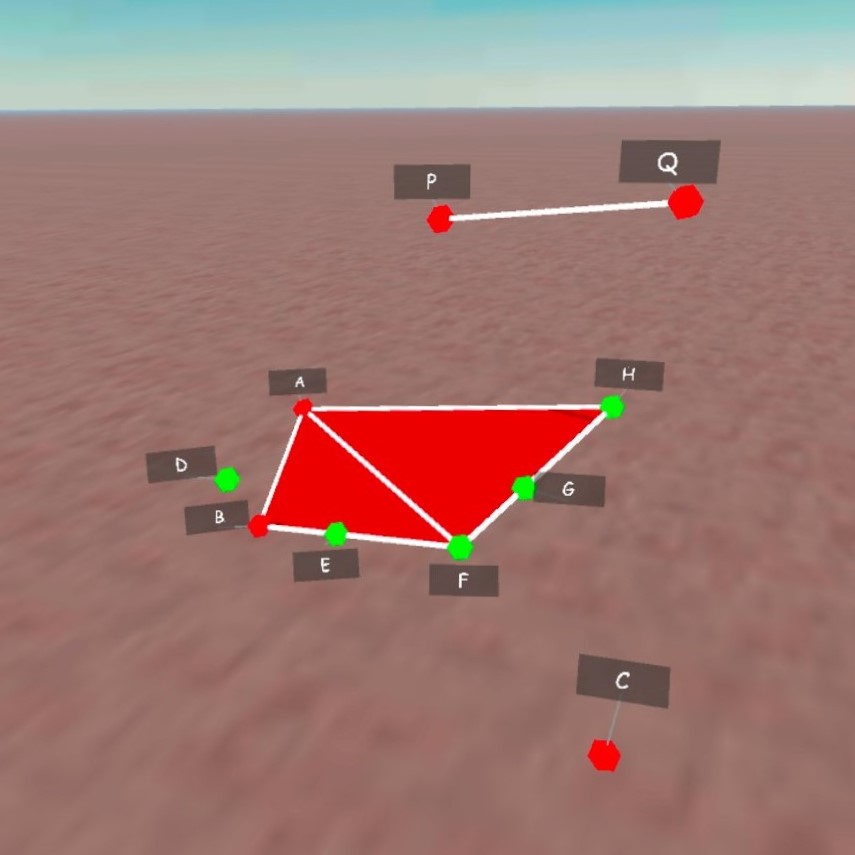
1. Empezamos con 3 puntos A, B, C.
2. Aparte, hacemos el segmento PQ que nos fijará la longitud del lado menor de todos los triángulos rectángulos de la espiral.
3. Con la herramienta perpendicular tocamos los vértices A, B, C para obtener un vértice D que nos dará la dirección perpendicular a dicho plano en B.
4. Tocamos A, B, D, para obtener un vértice E perpendicular a la arista AB, contenida en el plano ABC.
5. Con la herramienta compás (modo 0), tocamos P, Q, B, E. Eso nos dará un vértice F, tal que ABF es el triángulo rectángulo deseado.
6. Realizamos el triángulo ABF con el modo cara (triángulo) de la mano.
7. Para facilitar la construcción de las siguientes perpendiculares, todas ellas contenidas en el plano ABC, o ABF (que es el mismo), elegimos la opción “Plane geometry” en la herramienta de perpendiculares y tocamos el plano ABF.
8. Tocamos con la herramienta de perpendiculares el vértice F y la arista AF para dar un nuevo vértice G y seguir la construcción indicada en el siguiente video para construir el triángulo AFH.

Sigue el hilo de esta actividad en Twitter.