Ayer empezamos apilando balas de cañón sobre una base triangular (equilateral) y preguntábamos cuantas había. Después lo hicimos sobre una base cuadrada.
La solución nos la da el número tetraédrico T_5=35. En general, el N-ésimo número tetraédrico es la suma de los N primeros números triangulares N(N+1)/2, que coincide con N(N+1)(N+2)/6.
Una vez que averiguáis que el resultado es la suma de los 5 primeros cuadrados, esto es 55, en general 1^2+2^2+….+N^2=N(1+N)(2N+1)/6, se puede plantear el problema famoso sobre balas de cañón que consiste en encontrar un número cuadrado de balas M^2 que se apilen de forma piramidal, es decir N(1+N)(2N+1)/6 =M^2.
A parte de N=1, existe una única solución que es N=24, M=70
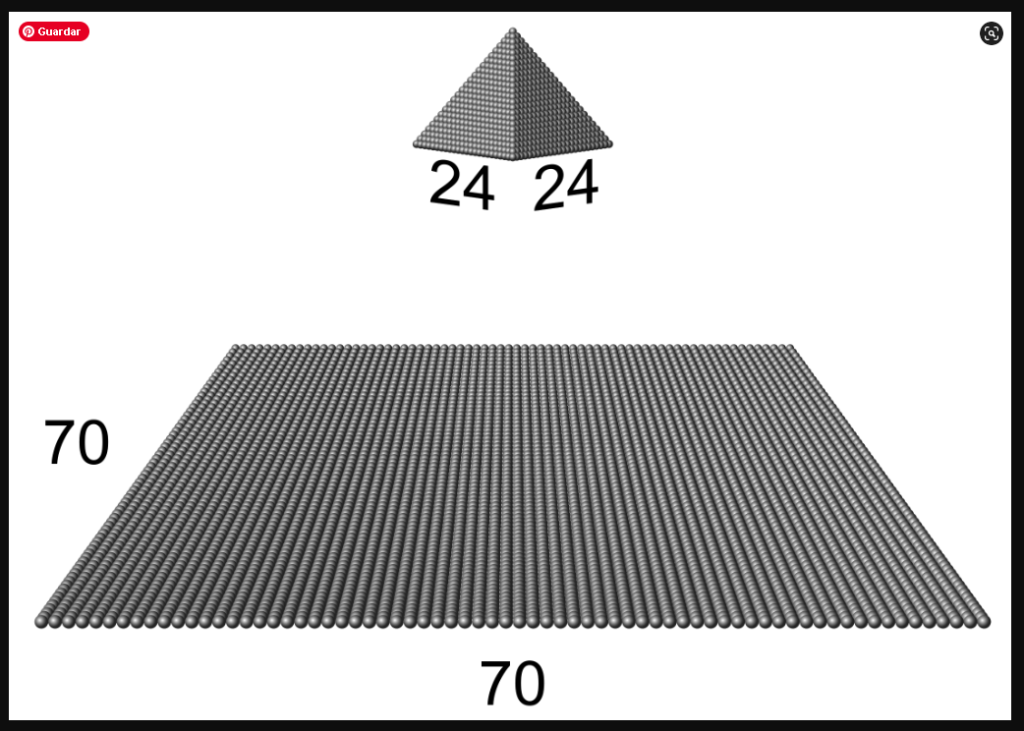
Más información sobre este problema:
¿Algún voluntario para disparar 4900 veces la pistola? Quizá implementemos una función que dispare automáticamente un número dado de balas… aunque no creo que lo soporte el juego. Podría servir para diseñar Máquinas de Galton, en 2 y 3d.
