Una figura geométrica es un conjunto no vacío y cerrado de puntos, delimitados por un conjunto de líneas (lados) que unen dichos puntos de una manera específica.
Las primeras figuras geométricas que conocemos son las figuras en dos dimensiones. Entre ellas, encontramos los polígonos y la circunferencia (cuyo interior es lo que denominamos círculo).
Un polígono es una figura geométrica plana delimitada por líneas rectas que encierran una región en el plano.
Triángulo

Se llama triángulo, en geometría plana, al polígono de tres lados. Es la figura geométrica más sencilla que podemos encontrar en el plano. Los puntos comunes a cada par de lados se denominan vértices.
Por la medida de sus lados, un triángulo puede ser equilátero (todos los lados iguales), isósceles (dos lados iguales y otro desigual) o escaleno (todos los lados desiguales).
Los ángulos interiores de un triángulo suman 180 grados.
Cuadrilátero

Un cuadrilátero es un polígono con cuatro lados y cuatro vértices.
Los ángulos interiores de un cuadrilátero suman 360 grados.
Cuando todos sus lados son iguales y todos sus ángulos interiores son rectos (90º) se trata de un cuadrado.
Pentágono

Un pentágono es un polígono con cinco lados y cinco vértices.
Cuando todos sus lados y ángulos son iguales, diremos que es un pentágono regular.
Los ángulos interiores de un pentágono siempre suman 540 grados.
Hexágono

Un hexágono es un polígono de seis lados y seis vértices.
Cuando todos sus lados y ángulos son iguales, diremos que es un hexágono regular.
Los ángulos interiores de un hexágono siempre suman 720 grados.
Círculo

El círculo es la región del plano formada por todos aquellos puntos cuya distancia a cierto punto fijo, conocido como centro, es menor o igual que cierta constante, conocida como radio.
Alternativamente, un círculo es la región del plano determinada por una circunferencia.
Es conveniente, por tanto, no confundir círculo con circunferencia; esta es solo el borde del círculo.
Estrella

Un polígono estrellado es un polígono regular (lados y vértices iguales) con forma de estrella que se obtiene de unir de forma no consecutiva los vértices de un polígono regular.
En el caso de la planta objeto de estudio, estamos ante un heptágono regular estrellado que, además, recibe el nombre de estrella de siete puntas o heptagrama.
Las geometrías en nuestro jardín
Podemos observar todo tipo de figuras geométricas en nuestro jardín. La Euphorbia obesa presenta una forma circular.

Las hojas de la Oxalis triangularis tienen forma de triángulo, como su nombre indica.

La Astrophynum Myriostigma tiene variantes interesantes desde el punto de vista geométrico, como la Astrophynum Myriostigma «quadricostatum».

Y la Astrophynum Myriostigma «pentacostatum».

La Euphorbia canariensis, símbolo natural de las Islas Canarias, presenta tallos hexagonales.

Y los tallos de la Cereus stegonus presentan la forma de una estrella de seis puntas.

Experimenta la geometría
Con lo que has aprendido, ahora puedes ponerte a prueba jugando.
- Nivel 1. Kahoot «Cuenta las figuras geométricas».
¿Nunca has jugado a Kahoot? Estas son las instrucciones para jugar una partida.
- Nivel 2. Resuelve el acertijo geométrico.
En nuestro acertijo podemos encontrar varios cuadrados, y un triángulo muy particular, llamado triángulo rectángulo. Se llama así porque tiene un ángulo recto, el que coincide con el del cuadrado. El lado más largo de este triángulo se llama hipotenusa (h), y los otros dos, catetos (a y b).
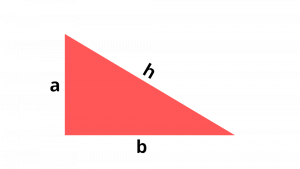
Lo más interesante es que las longitudes de sus lados están relacionados según el Teorema de Pitágoras: «En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos», o lo que es lo mismo:
h^2=a^2+b^2
Sabiendo esto, halla el área de las figuras con el área sombreada.

¿Necesitas una pista? Puedes verla aquí.
- Nivel 3. Introducción a la demostración.
El Teorema de Pitágoras, mencionado anteriormente, nos resulta muy útil para a la hora de demostrar resultados y resolver problemas matemáticos. Pero para estar seguros de que un teorema es cierto, alguien debe haberlo demostrado. En este caso no hay problema, ya que es uno de los teoremas con mayor número de demostraciones que existen. Puedes ver algunas de ellas aquí.