Se define como ángulo a la porción del plano limitada por dos semirrectas con origen en un mismo punto:
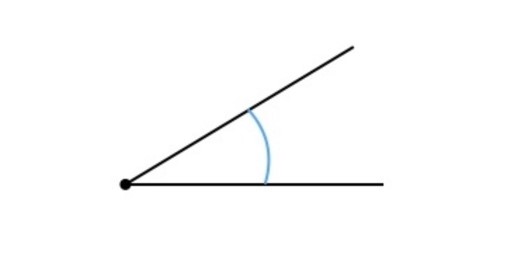
A las semirrectas se les llama lados inicial y final, y al origen común, vértice del ángulo. Si dibujamos el ángulo en un sistema cartesiano de coordenadas se suele hacer coincidir el vértice del ángulo con el origen de coordenadas y el lado inicial con el eje positivo de abscisas:
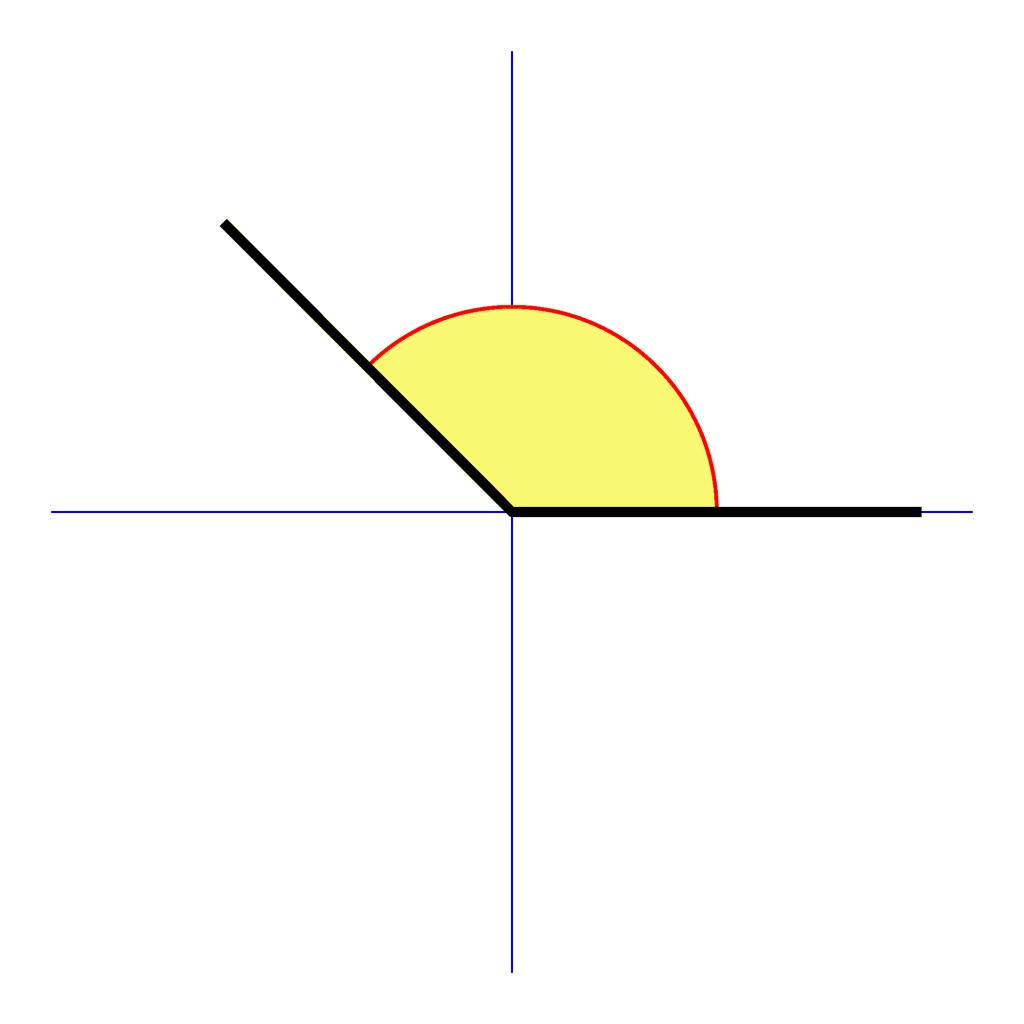
Los ángulos positivos se miden en sentido contrario a las agujas del reloj; en cambio, los negativos, en sentido horario.
Los ángulos se suelen medir en grados o en radianes. En el caso de la medición en grados, su valor oscila entre 0 y 360 grados (y los valores en 0 y 360 grados coinciden). Para referirnos a ellos, podemos escribir 90 grados, o lo que es lo mismo, 90º.
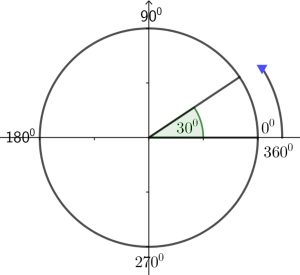
En el caso de la medición en radianes, su valor oscila entre 0 y 2π radianes, siendo un radián el ángulo cuyo vértice hacemos coincidir con el centro de una circunferencia y cuyo arco tiene longitud igual al radio de la circunferencia.
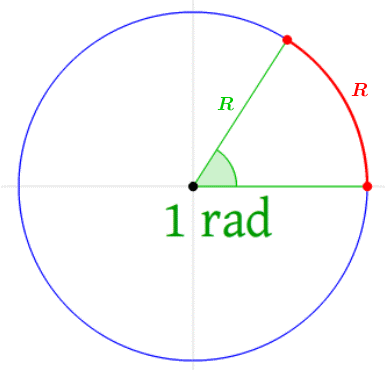
De esta manera, la equivalencia entre grados y radianes es la siguiente:
2π rad = 360º
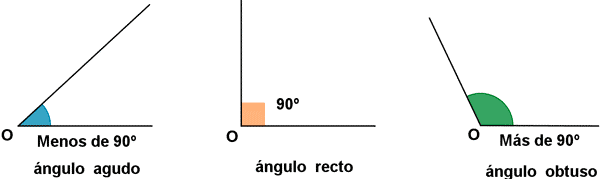
Por otro lado, los ángulos se pueden clasificar según su medida:
- Ángulo agudo: el que mide entre 0º y 90º (0 y π/2 rad).
- Ángulo recto: el que mide exactamente 90º (π/2 rad).
- Ángulo obtuso: el que mide entre 90º y 180º (π/2 rad y π rad).
Dentro de los ángulos obtusos hay uno en particular que es de gran interés en botánica: el ángulo áureo. Este ángulo tiene una estrecha relación con la sucesión de Fibonacci. Puede demostrarse que la sucesión de los cocientes de sus términos consecutivos (1, 2, 3, 5, 8, 13,…) es convergente al número áureo \Phi=\frac{1+\sqrt{5}}{2} .
lím_{n\rightarrow \infty} \frac{r_n}{r_{n-1}}=\Phi
Hay otra forma de definir el número áureo. Si queremos dividir la longitud de una circunferencia en dos ángulos, a y b, de manera que la proporción cumpla \frac{360}{a}=\frac{a}{b}:
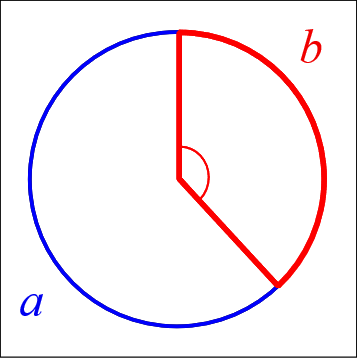
Se puede comprobar que dicha proporción es igual al número áureo, siendo el valor de los ángulos:
a=222,492235… b=137,507764…
A este último ángulo b se le denomina ángulo áureo, y aparece múltiples veces en el estudio de la disposición de distintas partes de la planta.
Ángulos en nuestro jardín
Podemos observar los distintos tipos de ángulos mencionados anteriormente en nuestro jardín.
El ángulo formado entre las ramas y el tronco de la Aucaria heterophylla (Salisb.) es un ángulo recto.

La Euphorbia tirucalli es un arbusto muy ramificado con ramas generalmente verticiladas, que forman entre sí ángulos agudos.

Podemos observar ángulos obstusos en las ramificaciones zigzagueantes de la Launaea arborescens.

Y por último, mencionamos la Aloe maculata, una planta en roseta con hojas formando espiral a lo largo del tallo, cuyas hojas consecutivas forman un ángulo aproximadamente igual al áureo.

Experimenta los ángulos
A continuación se presentan algunas actividades para que podáis disfrutar con las matemáticas de nuestro jardín.
1. Busca entre las plantas ubicadas en cada uno de los jardines patrones de regularidad en lo que se refiere a los ángulos. Por ejemplo, el ángulo entre el tallo o tronco y sus ramas, o bien, entre las ramas y sus hojas, o también entre los pétalos de una flor.
Una vez detectado un patrón en la planta (por ejemplo, si todos los ángulos son agudos), hazle una foto o vídeo en el que se vea los más claramente posible los ángulos formados y cómo se repiten.
2. Fotografía desde arriba (como en la web del jardín) la planta aloe maculata y comprueba visualmente que sus hojas forman una espiral a lo largo del eje vertical que pasa por el centro, siendo las últimas hojas en salir las interiores. Además, comprueba que efectivamente el ángulo existente entre hojas consecutivas es siempre aproximadamente igual al ángulo áureo.
3. La distribución de las hojas en un tallo es helicoidal cuando cada hoja está girada respecto a la anterior en un ángulo inferior a 180º. Si nos fijamos en el tallo en la hoja más baja y contamos “m” hojas dando “n” vueltas alrededor del tallo hasta alcanzar la hoja que está superpuesta a la hoja de partida, obtenemos la fracción: n / m.
El ángulo de divergencia viene dado por n / m x 360º , el cual coincide con el ángulo existente entre cada dos hojas consecutivas del tallo. Busca plantas en las que se pueda determinar su ángulo divergencia.
Haz una foto o vídeo en la se vean el número de hojas necesarias para que una hoja se superponga a otra.
Te animamos a que la subas a Twitter o Instagram y nos etiquetes (@experiment_UAL en Twitter, @facultad.experimentales.ual en Instagram).
Se puede ampliar la búsqueda fuera de los jardines matemáticos de la UAL.