«La belleza depende tanto del tamaño como de la simetría» (Aristóteles, 384-322 a. C.)
A lo largo de la historia, la simetría se ha visto como un canon de belleza y perfección a niveles de proporción, también denominada para los antiguos griegos, la «divina proporción», donde relacionaban conceptos de armonía y matemáticas. La simetría se ha plasmado, no solo en obras de arte y en arquitectura, como vemos en el legado del Imperio Romano, creando tendencia al colosalismo y al predominio de la regularidad; sino que también es un bien propio de la naturaleza que nos rodea, según recogen los renacentistas, creyendo que es algo digno de imitar por ser creación divina. Con la simetría se ordena la forma total para que aparezca la belleza de lo natural.
Por lo tanto, podemos definir la simetría como la proporción que hay en un objeto o entre objetos pero, ¿respecto de qué? Pues respecto de un centro, eje o plano.
Existen, principalmente, tres tipos de simetría:
- Simetría central. Dado un punto, al que llamamos centro de simetría, se produce un objeto de modo que a cada punto le corresponde otro situado a la misma distancia respecto del centro.
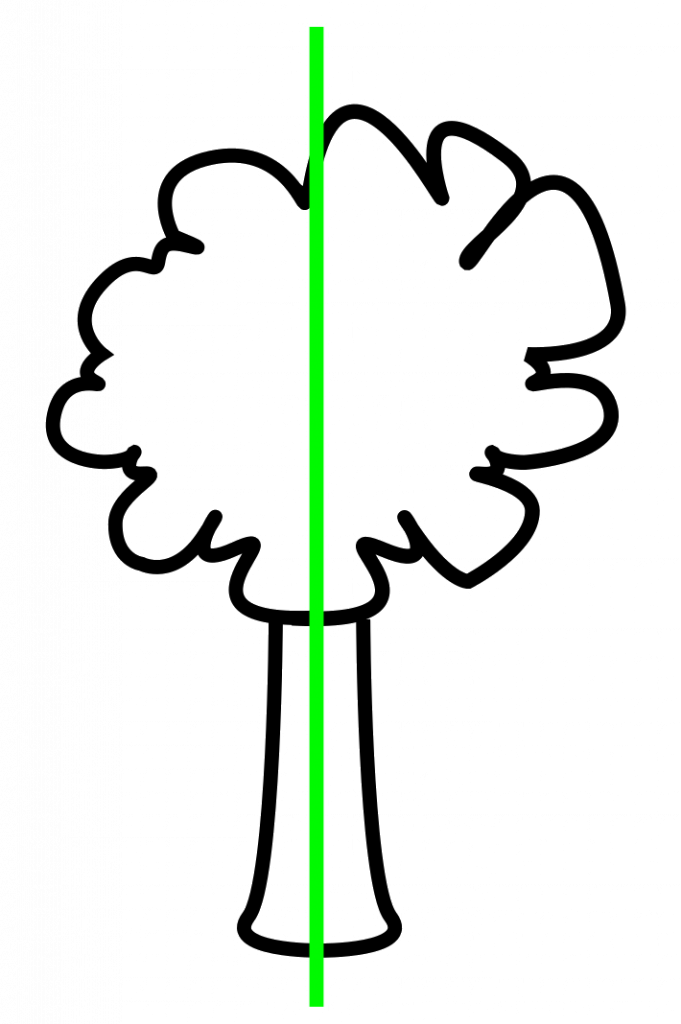
- Simetría axial. También llamada bilateral. Dada una línea, a la que denominaremos eje de simetría, consiste en reproducir un objeto de modo que a cada punto del objeto original le corresponde otro situado a la misma distancia respecto del eje, y el punto medio del segmento que forman el punto del objeto original y el correspondiente de la copia está situado en dicho eje.
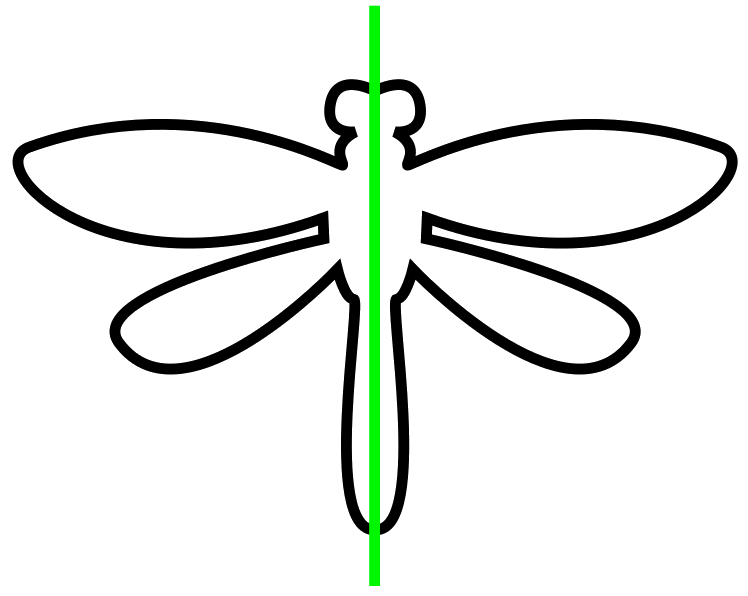
- Simetría radial. También llamada rotacional. Dado un objeto, este puede girarse respecto a sí mismo y no varía. Es decir, situado el centro del objeto, si se rota dicho objeto respecto del centro se obtiene la figura original sin tener que haber rotado totalmente, 360º.
Simetría radial
«La belleza es nuestra arma contra la naturaleza, por ello hacemos objetos, dándoles límite, simetría, proporción. Detiene Belleza y congela el flujo de fusión de la naturaleza» (Camile Paglia, 1947)
Como hemos visto, la Simetría radial o rotacional se produce cuando un objeto puede girarse respecto a sí mismo y no varía.
En la Alhambra de Granada, y más cerca de nosotros, en la Alcazaba de Almería, podemos encontrar objetos formando rosáceas (figuras que van ampliándose desde su centro por traslación), frisos (parte de la figura replicada en una dirección) y mosaicos (replicación de partes de figuras en dos direcciones diferentes). Los diseñadores de estas geometrías crearon belleza a partir de la simetría radial.
Para estas estructuras, podemos hablar de conceptos tan importantes como:
– Centro de rotación. Es el centro del objeto, desde donde se puede dibujar una línea imaginaria y que, al girar sobre ella, se produce la rotación.
– Simetría de orden n, y en particular, la simetría rotacional de n-pliegues. El orden de simetría es el número de veces que podemos obtener el mismo objeto antes de dar la vuelta entera de 360º.
– Grados de rotación. Es el número de grados (ángulo) que un objeto puede ser rotado alrededor de su centro. Los órdenes están estrechamente relacionados con los ángulos.
- Orden 2: 180º = 360º/2
- Orden 3: 120º = 360º/3
- Orden 4: 90º = 360º/4
- …
- Orden n: 360º/n
Veamos algunos ejemplos de figuras geométricas. Un triángulo equilátero tiene orden de rotación 3.
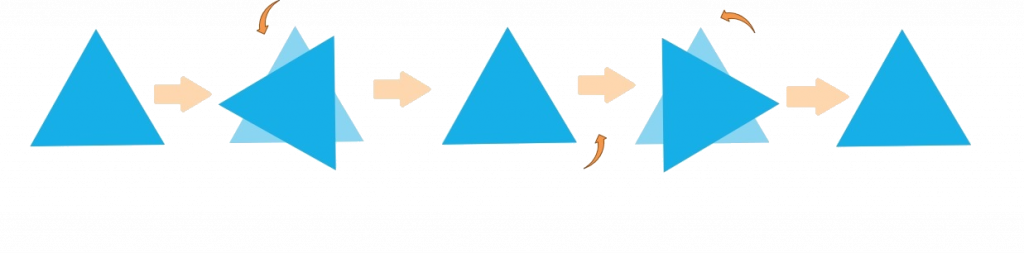
Un cuadrado tiene orden de rotación 4.

Un pentágono tiene orden de rotación 5.

Asimetría
No todo en la Antigua Grecia era proporción. El menos en cuanto a indumentaria se refería: una túnica rectangular de lino o lana sujeta a una hebilla sobre el hombro derecho que cae formando pliegues; en la arquitectura con el templo de Erecteón hasta, más recientemente, los alicatados de la Alhambra de Granada; en todo ello podemos encontrar la llamada asimetría cromática.
Hay varias maneras de definir la asimetría, pero nos centraremos en las dos más importantes:
1. La Asimetría como falta de proporción, de armonía, en un objeto. Esto es, la ausencia de simetría.
2. La Asimetría con respecto a un centro o a un eje.
- Asimetría central. Dado un punto, al que llamamos centro de asimetría, se reproducen objetos en contraposición, es decir, a cada punto le corresponde su opuesto situado a la misma distancia respecto del centro.
- Asimetría axial. Dado un eje, se reproducen objetos pero partiendo de uno en común, de modo que a cada punto se le hace corresponder su opuesto situado a la misma distancia respecto de un eje, y el punto medio del segmento que forman está situado en dicho eje.
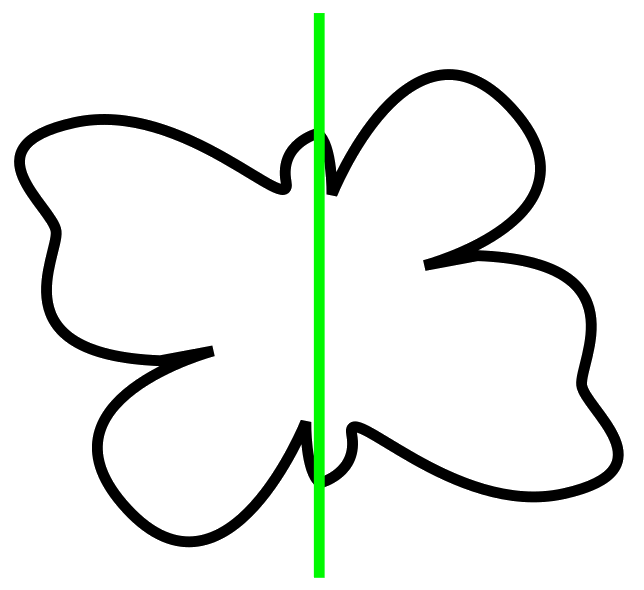
Simetrías en la Dietes bicolor
La flor de la Dietes bicolor tiene mucho interés desde el punto de vista de las simetrías, por la forma en que aparecen sus pétalos. Si dibujamos una línea que pase por el centro y la punta de uno de sus pétalos más grandes, situados en la base, obtenemos que cada parte en la que dicha línea recta divide la flor es el reflejo de la otra. Esto nos dice que esta flor presenta simetría axial.

Pero esta no es la única simetría que podemos encontrar en ella. Si tomamos el centro de la flor y la giramos respecto a este punto hasta completar una vuelta, primero hasta alcanzar un ángulo de 120º, luego 240º, y finalmente 360º, observamos que no hay variación. La flor de la Dietes bicolor tiene simetría radial o rotacional.

Por otro lado, en la Naturaleza encontramos innumerables ejemplos de asimetría. Uno que podemos ver en nuestro jardín es la Cereus peruvianus monstruosus o cactus monstruoso, una planta que puede superar los siete metros de altura, con abundantes ramificaciones de las que surgen protuberancias con crestas que dan lugar a formar retorcidas y muy diferentes entre sí, denominadas costillas.

Experimenta las simetrías
Con lo que has aprendido, ahora puedes ponerte a prueba jugando un Kahoot. Hay tres niveles diferentes, ¿conseguirás superarlos?
- Nivel 1: Encuentra la simetría
- Nivel 2: Encuentra el ángulo de rotación
- Nivel 3: Avanzado
¿Nunca has jugado a Kahoot? Estas son las instrucciones para jugar una partida.