Hélices
Una hélice es una curva C en el espacio de manera que, respecto a una recta r fijada, la recta tangente a cada punto de C forma un ángulo constante con la recta r.
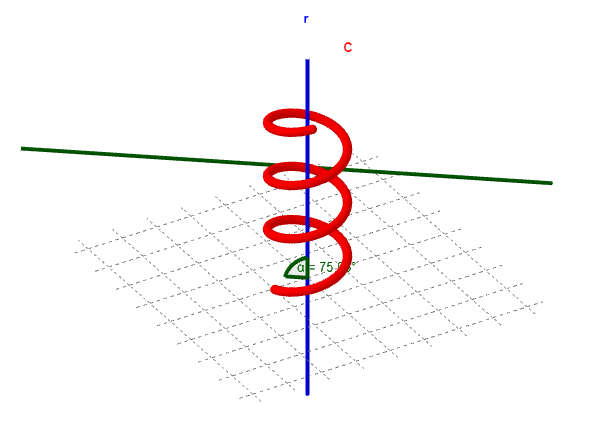
(puede verse la animación en este enlace). Salvo cambios de escala, rotaciones o traslaciones, toda hélice (recorrida en sentido horario) puede reducirse a las siguientes ecuaciones paramétricas:
\begin{aligned}
x(t)&=\rho \ cos(t) \\
y(t)&=\rho \ sen(t) \\
z(t)&= ct
\end{aligned}En este caso se trata de una hélice cilíndrica de radio \rho y altura 2\pi c. También se denomina hélice circular de curvatura \frac{\rho}{\rho^2+c^2} y torsión \frac{c}{\rho^2+c^2}.
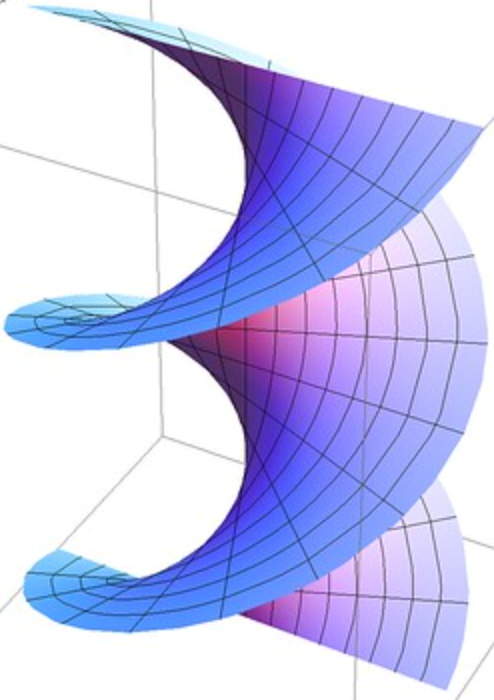
La superficie de menor área que tiene a la hélice como frontera se denomina helicoide.
Espirales
Una espiral es una línea curva generada por un punto que se va alejando progresivamente del centro a la vez que gira alrededor de él. Normalmente se define con una función que depende de dos valores: el ángulo del punto respecto a un eje de referencia, y la distancia desde este punto al centro, situado en el vértice del ángulo.
Su expresión matemática se puede resumir en la fórmula uniparamétrica:
t \rightarrow t exp(it)
con t>0 e i la unidad imaginaria, que expresa cómo el punto
(t, t exp(it)) combina su alejamiento progresivo del origen mientras que gira alrededor del mismo.
Son muy diversas y famosas las posibles formas de espirales: de Arquímedes, logarítmica, hiperbólica, de Fermat…
Ha jugado un papel simbólico muy importante en todas las culturas desde el Megalítico.
La espiral no debe confundirse con la hélice: la segunda es tridimensional, mientras que la primera es plana; si bien están estrechamente relacionadas.
Hélices y espirales en nuestro jardín
En nuestro jardín podemos observar que la Cereus forbesii «spiralis» presenta forma de hélice.

Al igual que la Juncus effusus «spiralis».

Podemos encontrar espirales en cómo se distribuyen los piñones de una piña, las hojas de una rosa o el disco floral en los girasoles. En sentido estricto, aquí se conectarían espirales y hélices, pues ninguno de estos casos es el de una curva plana, que sería en teoría.
En nuestro jardín podemos observar espirales en la Sulcorebutia.

Experimenta las espirales
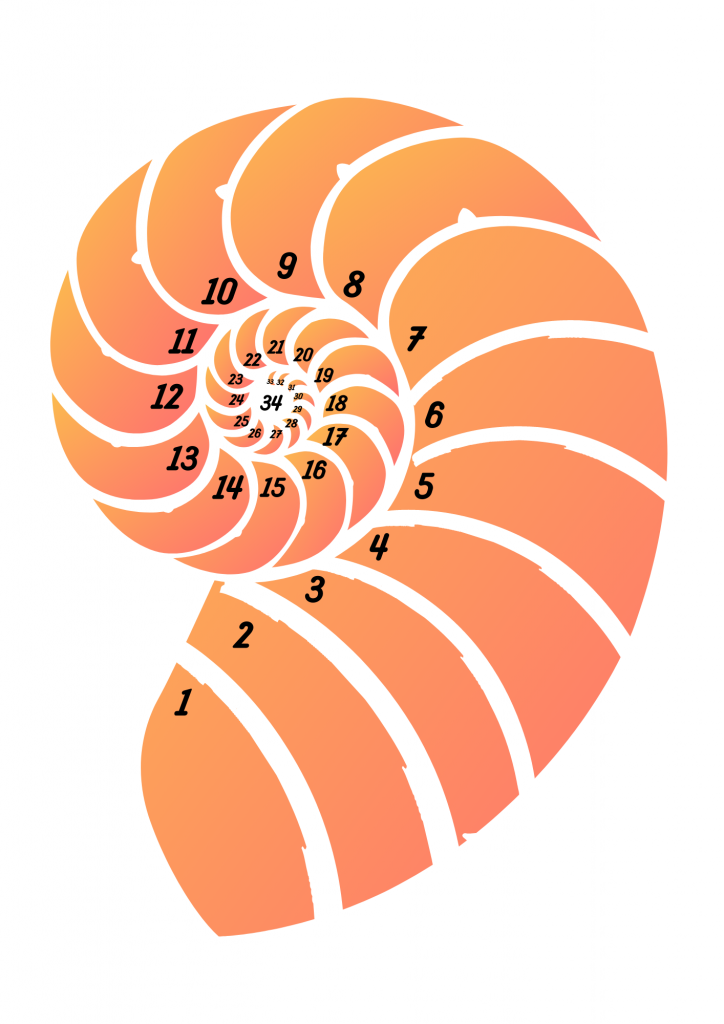
¿Conoces la espiral de Fibonacci? También es conocida como espiral dorada, y se genera dibujando arcos circulares que conectan las esquinas opuestas de cuadrados cuyos lados tienen como longitud los términos de la sucesión de Fibonacci.
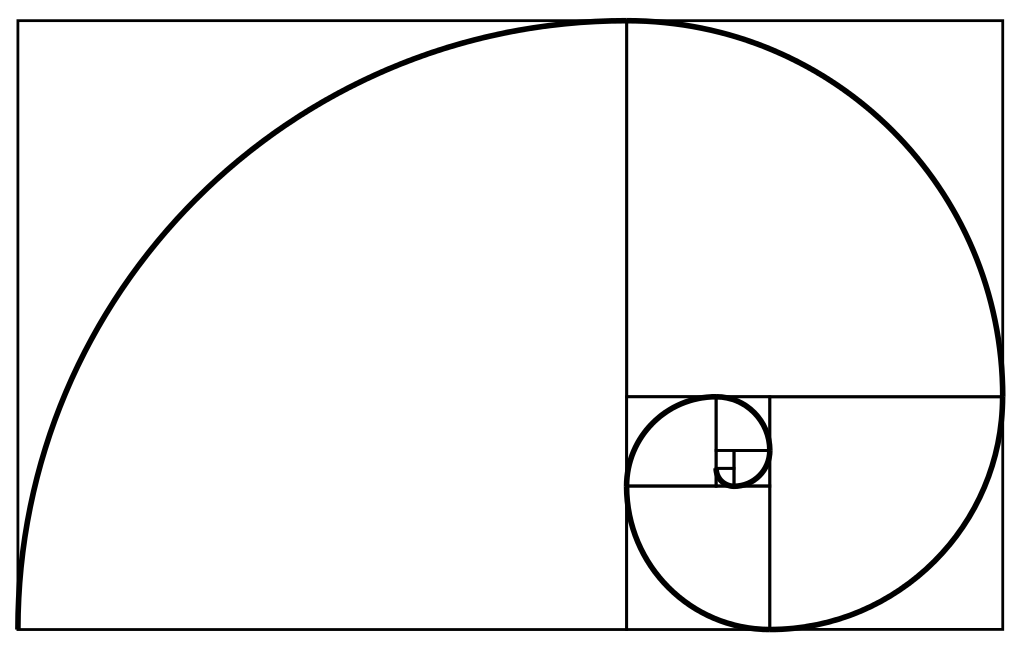
En este caso aparece representada una espiral con ocho cuadrados, con lo que sus lados tienen los 8 primeros términos de la sucesión.
A continuación se presenta un juego de mesa, que contiene también los 8 primeros términos de la sucesión. La dinámica es similar a la oca, y el objetivo es llegar hasta el octavo término, que se encuentra en el centro. Pero en este caso lo que nos permite avanzar con mayor velocidad no son las ocas, sino caer en casillas cuyo número pertenezca a la sucesión de Fibonacci. Debes estar muy atent@, pues no están marcadas. ¡Disfruta con este juego en espiral!