«Cada curva matemática tiene una naturaleza propia, la exactitud de una ley, la expresión de una idea, la evidencia de una virtud» (Eduardo Torroja Miret, 1899-1961).
¿Has visto la cantidad de flores que hay en nuestro jardín? ¡Dan ganas de dibujarlas todas! Hay de muchos colores diferentes, pero, sin duda, lo que nos permite diferenciar unas de otras es el número de pétalos y sus formas. Cuando dibujamos una flor, lo que normalmente hacemos es colocar sus pétalos alrededor del centro, haciendo curvas en el papel, pero, ¿sabías que con las matemáticas podemos dibujar todas las flores que hay en la Naturaleza? ¡Ahora mismo te lo explicamos!
Desde la Antigua Grecia se han intentado resolver problemas en los que aparecen involucradas diferentes curvas, como la cuadratura del círculo, la trisección de un ángulo, o la duplicación del cubo usando regla y compás.
En 1728, el profesor de la Universidad de Pisa Guido Grandi (1671-1742) publicó su obra Flores geometrici, el primer tratado en el cual se presenta y describe una familia de curvas muy similares a las flores que podemos ver a nuestro alrededor. Dichas curvas reciben el nombre de concoide de rosetón o pétalo geométrico.
Obtener la forma general de los puntos que componen estas curvas es muy sencillo: observemos que cuando dibujamos nuestra flor, lo hacemos en una superficie plana, por lo que los puntos de los que se compondrá cada curva tendrán dos coordenadas: una horizontal y otra vertical. Sin embargo, en la definición de la concoide de rosetón no vamos a trabajar directamente con las clásicas coordenadas cartesianas (x,y), ya que harían las expresiones de las curvas bastante complejas y sería difícil trabajar con ellas. En su lugar, utilizaremos otro tipo de coordenadas descubiertas por Galileo (1564-1642) y Cavalieri (1598-1647), que facilitaron la representación de curvas y superficies. En ellas se tiene en cuenta la distancia del punto al origen de coordenadas, a la que llamaremos ρ, y el ángulo de giro respecto del eje horizontal, θ, el cual puede oscilar desde los –π radianes hasta los π. Cada punto (x,y) de la curva tiene un par (ρ, θ) asociado a él, que denominamos coordenadas polares. Además, podemos expresar x e y en función de ρ y θ como se muestra en la siguiente imagen, lo que se conoce en matemáticas como cambio de coordenadas polares a coordenadas cartesianas:
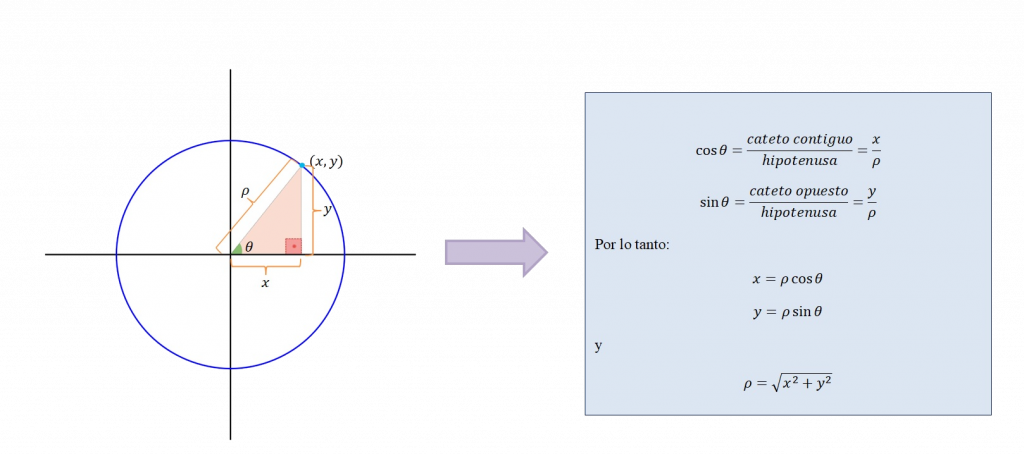
Para la concoide de rosetón, se tiene la siguiente relación entre ρ y θ:
ρ=a cos(nθ)+b, \quad -\frac{\pi}{n}\leq θ \leq \frac{\pi}{n}
donde los parámetros a y b pueden tomar cualquier valor, y n es un número real mayor que cero. Así, los puntos que compondrán la curva, expresados en coordenadas polares, serán:
(a cos(nθ)+b, θ)
Cambiando los valores de los parámetros en cada representación, podremos obtener los dibujos de las diferentes flores. Para esta tarea contamos en la actualidad con programas de ordenador que tratan fácil y rápidamente la representación de los puntos de la curva.
La begonia y el concoide de rosetón
A pesar de ser una planta bastante pequeña, la Begonia semperflorens llama la atención por sus abundantes flores de colores muy variados.
Gracias a la familia de curvas que engloba la concoide de rosetón, podemos dibujar los pétalos de esta flor de nuestro jardín. Observemos, en primer lugar, la peculiar forma de su corola:

Alrededor de su centro, tenemos dos pétalos más grandes y anchos, y otros dos de menor tamaño y estrechos situados en ambos casos en lados opuestos. Para dibujar nuestra flor utilizando nuestros conocimientos de la concoide de rosetón, sabemos que hemos de representar los puntos de la siguiente manera:
(a cos (n\theta) +b, \theta), \quad 0 \leq \theta \leq 2\pi
siendo a,b y n números reales. Pero, ¿qué valores de a,b y n se adapta a la forma de la begonia? Para saberlo, hemos de estudiar distintos casos:
– Si a>b>0, las flores que se representan con los puntos anteriores presentan unos pétalos que se disponen alrededor de un centro consistente solo en un punto. Atendiendo al valor de n, podemos encontrarno s con diferentes situaciones:
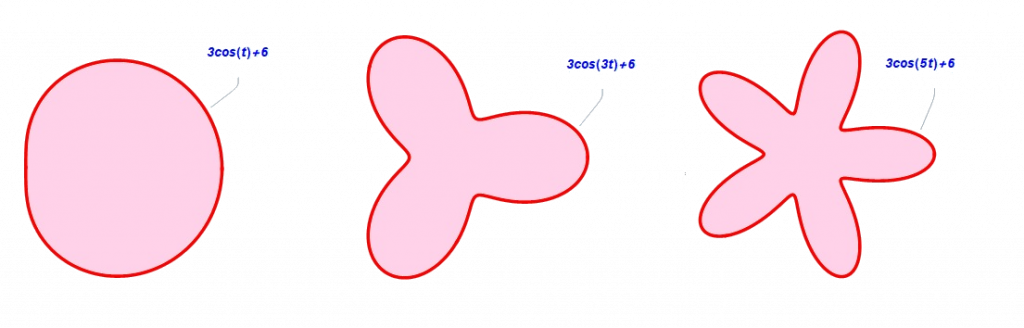
- Si n es un número natural, n=1,2,3,4,..., entonces obtendremos un número de pétalos igual al doble de n, siendo una mitad de ellos de tamaño menor que los otros. Si n es par, los pétalos grandes y pequeños se van intercalando, y si n es impar, los pétalos pequeños se encuentran sobre los más grandes.
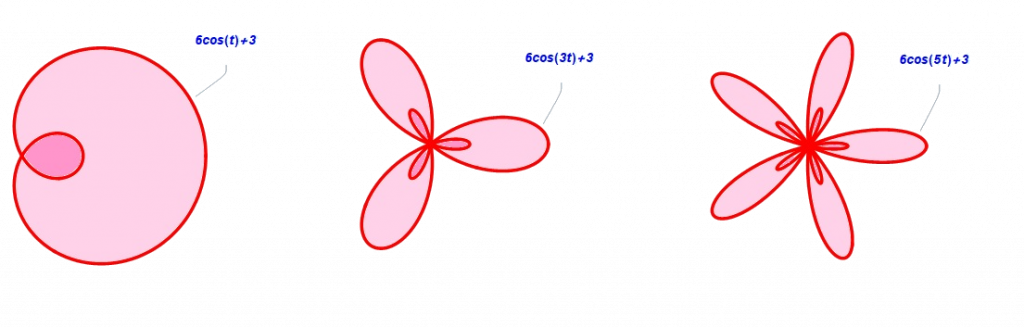
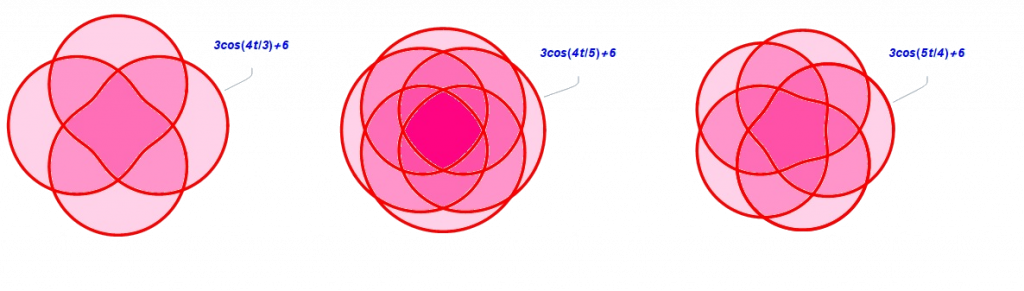
- Si n no es natural, de manera que podemos expresarlo como n=\frac{m}{p}, siendo m y p números tales que m no es múltiplo de p; entonces obtenemos una estructura en la que aparecen m pétalos de mayor tamaño, y sobre ellos, se va repitiendo la disposición del mismo número de pétalos que los primeros obtenidos, pero con diferentes giros y cada vez menor tamaño. El total de veces que se repite la estructura inicial de pétalos, contando estos, es p.

– Si a=b, los pétalos de nuestra flor se distribuyen girando alrededor de un mismo punto, que actúa de centro de la misma. Según los valores de n, tenemos que diferenciar dos casos, igual que antes.
- Si n es un número natural, entonces la corola de la flor estará compuesta por n pétalos, todos del mismo tamaño. Destacamos el caso n=1, que nos proporciona la representación de la famosa curva cardioide, llamada así por si parecido a un corazón.
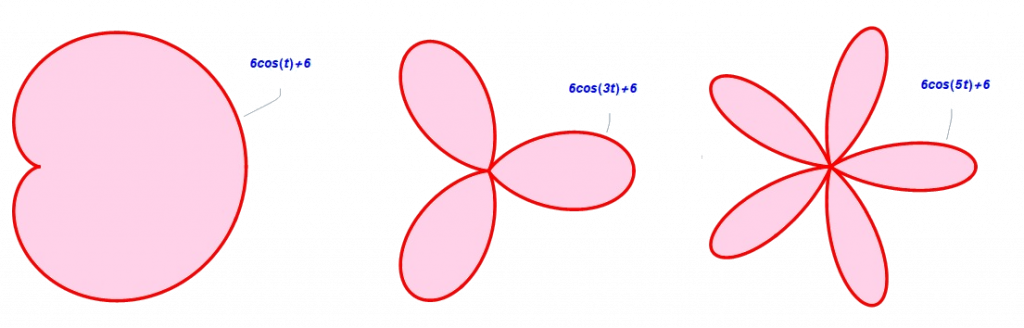
- Si n no es natural, de manera que podemos expresarlo como n=\frac{m}{p}, siendo m y p números tales que m no es múltiplo de p; entonces el resultado es muy similar al mismo caso para a>b>0, con la salvedad de que en este, los pétalos que se disponen encima de los más grandes cumplen que su punto más alejado del centro es un punto que comparten un pétalo sobre el que está situado y el siguiente, siendo dicho punto donde termina uno y empieza el otro.
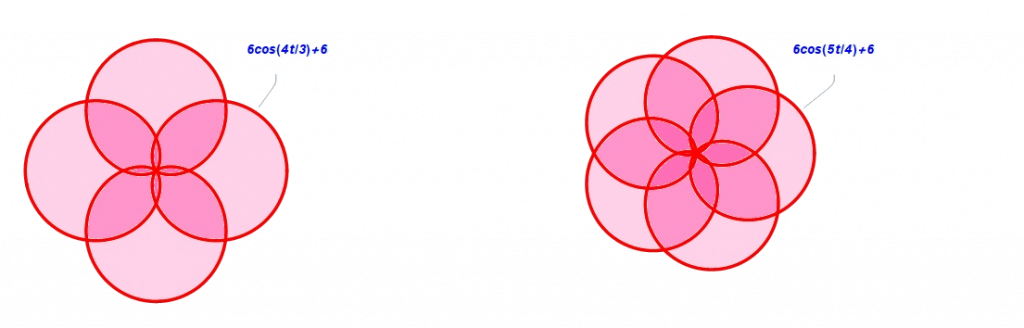
– Si a<b, se forman unos pétalos que se encuentran dispuestos alrededor de un centro que se construye como la circunferencia que deja inscrito un polígono regular cuyos vértices son los puntos de la curva en los que empieza o termina un pétalo y se acaba o se inicia otro.
- Si n es un número natural, entonces dibujaremos una flor que tiene exactamente n pétallos, y cuyo centro es de la forma anteriormente descrita. En el caso de que n=1, no tendrá sentido hablar del polígono que forma la parte del centro, al existir solamente un pétalo, y cuando n=2, en vez de hablar de circunferencia que describe un polígono regular, solamente tendremos un segmento, que será la parte que tengan los pétalos en común.
- Si n no es natural, de manera que podemos expresarlo como n=\frac{m}{p}, siendo m y p números tales que m no es múltiplo de p; entonces los pétalos se comportan de la misma forma que en el caso a=b, si bien hay que tener en cuenta la presencia de un centro mucho más amplio en este que estamos considerando.
De la descripción de la forma de la corola de la begonia, y de los casos que hemos visto para la concoide de rosetón, podemos deducir que la curva que mejor la representa es aquella en la que a>b>0 y n tiene el valor 2, como vemos también en la siguiente imagen.

Experimenta el concoide de rosetón
¿Te gustaría dibujar tus propias flores? Este programa te permitirá experimentar con los distintos valores de a, b y n. ¡Atrévete!
Con lo que has aprendido, ahora puedes ponerte a prueba jugando un Kahoot. Hay tres niveles diferentes, ¿conseguirás superarlos?
- Nivel 1: Encuentra la curva
- Nivel 2: Encuentra la flor
- Nivel 3: Encuentra los parámetros
¿Nunca has jugado a Kahoot? Estas son las instrucciones para jugar una partida.